
In making correlations between botany and the Fibonacci sequence (Peterson 2006). Numbers in botany is sometimes called Ludwig's law (Szymkiewicz 1928 Wells 1986, Sometimes called pine cone numbers (Pappas 1989, p. 224).
Of a plant ( phyllotaxis): for elm and linden, 1/3įor beech and hazel, 2/5 for oak and apple, 3/8 for poplar and rose, 5/13 for willowĪnd almond, etc. The convergents to, where is the golden ratio, andĪre said to measure the fraction of a turn between successive leaves on the stalk The ratios of alternate Fibonacci numbers are given by The ratios of successive Fibonacci numbers approaches the goldenĪpproaches infinity, as first proved by Scottish mathematician Robert Simson in 1753 (OEIS A037918).Īnd for all, and there is at least one such that. This follows from the fact thatįor any power function, the number of decimal digits for is given by. Strings of digits settle down to produce the number 208987640249978733769., whichĬorresponds to the decimal digits of (OEIS A097348), The numbers of Fibonacci numbers less than 10,. The number of such rhythms having beats altogether is, and hence these scholars both mentioned the numbersġ, 2, 3, 5, 8, 13, 21. Had long been interested in rhythmic patterns that are formed from one-beat and two-beat Before Fibonacci wrote his work, the Fibonacci numbers had already been discussedīy Indian scholars such as Gopāla (before 1135) and Hemachandra (c. KeplerĪlso described the Fibonacci numbers (Kepler 1966 Wells 1986, pp. 61-62 andĦ5). The Fibonacci numbers give the number of pairs of rabbits months after a single pair begins breeding (and newly bornīunnies are assumed to begin breeding when they are two months old), as first describedīy Leonardo of Pisa (also known as Fibonacci) in his book Liber Abaci. To the fact that the binary representation of ends in zeros.
#CALCULATE FIBONACCI SERIES#
The plot above shows the first 511 terms of the Fibonacci sequence represented in binary, revealing an interesting pattern of hollow and filled triangles (Pegg 2003).Ī fractal-like series of white triangles appears on the bottom edge, due in part Of the killings lie on the graph of a golden spiral,Īnd going to the center of the spiral allows Reid to determine the location of the In this episode, character Dr. Reid also notices that locations Who uses the Fibonacci sequence to determine the number of victims for each of his
#CALCULATE FIBONACCI SERIAL#
The agents of the FBI Behavioral Analysis Unit are confronted by a serial killer "Masterpiece" (2008) of the CBS-TV crime drama "Criminal Minds,"

Of crystals and the spiral of galaxies and a nautilus shell. Math genius Charlie Eppes mentions that the Fibonacci numbers are found in the structure (2005) of the television crime drama NUMB3RS,
#CALCULATE FIBONACCI CODE#
Museum curator Jacque Saunière in D. Brown's novel Theĭa Vinci Code (Brown 2003, pp. 43, 60-61, and 189-192). (The right panel instead applies the PerrinĪ scrambled version 13, 3, 2, 21, 1, 1, 8, 5 (OEIS A117540) of the first eight Fibonacci numbers appear as one of the clues left by murdered
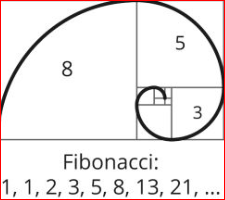
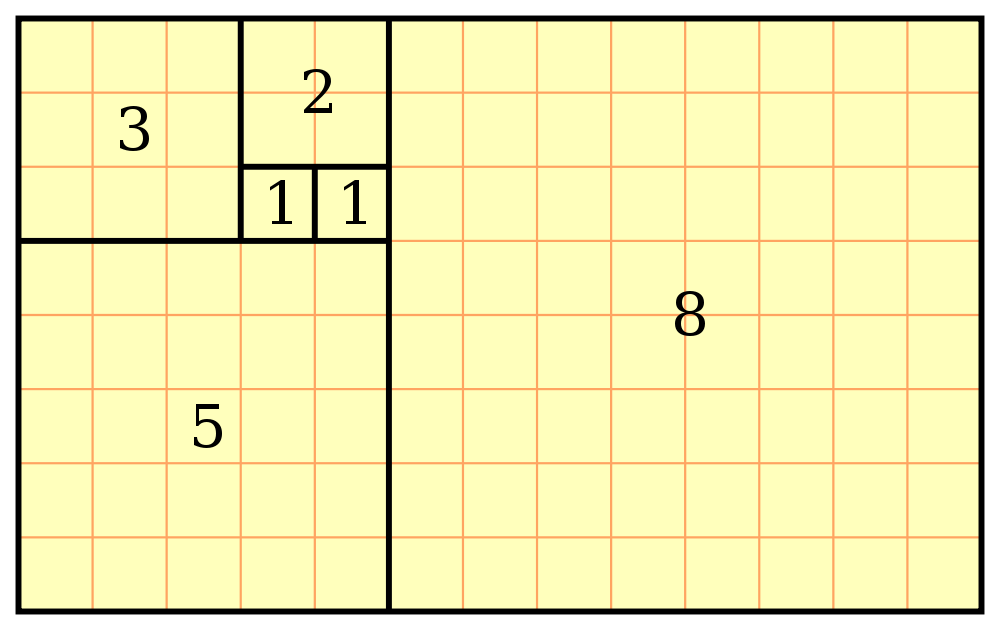
The above cartoon (Amend 2005) shows an unconventional sports application of the Fibonacci numbers (left two panels). The Fibonacci numbers are also a Lucas sequence, and are companions to the Lucas numbers (which satisfy the same recurrence (OEIS A000045).įibonacci numbers can be viewed as a particular case of the Fibonacci polynomialsįibonacci numbers are implemented in the Wolfram “Fibonacci Number Formula.” Math Fun Facts.As a result of the definition ( 1), it is conventional to define You can learn more about recurrence formulas in a fun course called discrete mathematics. It can also be proved using the eigenvalues of a 2×2- matrix that encodes the recurrence. This formula is attributed to Binet in 1843, though known by Euler before him. Phi = (1 – Sqrt) / 2 is an associated golden number, also equal to (-1 / Phi). Where Phi = (1 + Sqrt) / 2 is the so-called golden mean, and Yes, there is an exact formula for the n-th term! It is: However, if I wanted the 100th term of this sequence, it would take lots of intermediate calculations with the recursive formula to get a result. Thus the sequence begins: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, … This sequence of Fibonacci numbers arises all over mathematics and also in nature. The fibonacci numbers are generated by setting F 0 = 0, F 1 = 1, and then using the recursive formula


 0 kommentar(er)
0 kommentar(er)
